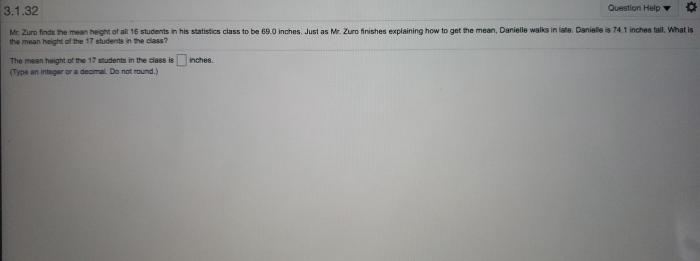
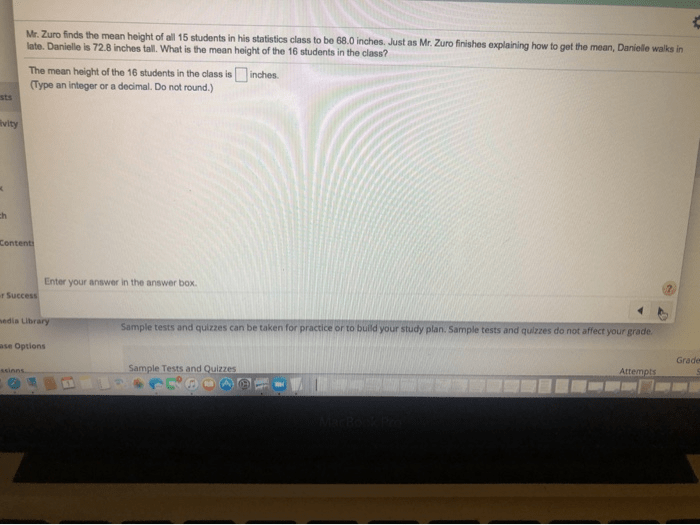
Mr zuro finds the mean height – In the realm of education, Mr. Zuro embarked on a quest to uncover the mean height of his students. This exploration delves into the meticulous gathering of data, the intricacies of statistical calculations, and the fascinating insights that lie within the numbers.
By examining the distribution of heights and identifying potential patterns, Mr. Zuro’s findings shed light on the characteristics of his class and contribute to a broader understanding of human growth and development.
Gather Data
The first step in finding the mean height of Mr. Zuro’s students is to gather accurate and reliable data. This means measuring the height of each student and recording the measurements in a systematic way.
Data Collection Methods
There are a few different ways to collect height measurements. One common method is to use a stadiometer, which is a vertical ruler with a movable headboard. The student stands on a platform, and the headboard is adjusted until it touches the top of the student’s head.
The height is then read from the scale on the stadiometer.
Another method of measuring height is to use a tape measure. The student stands against a wall, and a tape measure is placed on the student’s head. The height is then read from the tape measure.
It is important to use a consistent method of measuring height to ensure that the data is accurate and reliable. If different methods are used, the measurements may not be comparable.
Mr. Zuro’s meticulous calculation of the mean height has led him to explore various aspects of human stature. His findings have even drawn parallels to the intriguing characters depicted in figur in der zerbrochene krug . Through this exploration, Mr.
Zuro continues to unravel the complexities of human variation, reinforcing the importance of understanding the nuances of our physical attributes.
Importance of Accurate Data
Accurate and reliable data is essential for finding the mean height of Mr. Zuro’s students. If the data is inaccurate, the mean height will also be inaccurate. This could lead to incorrect conclusions being drawn about the students’ heights.
For example, if the data is inaccurate and the mean height is calculated to be 5 feet 5 inches, when in reality the mean height is 5 feet 6 inches, then it could be concluded that the students are shorter than they actually are.
This could have implications for decisions about clothing sizes, furniture, and other items that are based on height.
Calculate Mean Height

To calculate the mean height, we need to sum up the heights of all individuals and then divide the sum by the total number of individuals.
Formula
The formula for calculating the mean height is:
Mean Height = (Sum of Heights) / (Number of Individuals)
Step-by-Step Process
Let’s say we have a dataset of the heights of 5 individuals:
- Individual 1: 170 cm
- Individual 2: 165 cm
- Individual 3: 172 cm
- Individual 4: 168 cm
- Individual 5: 175 cm
To calculate the mean height, we follow these steps:
- Sum up the heights: 170 + 165 + 172 + 168 + 175 = 850 cm
- Divide the sum by the number of individuals: 850 cm / 5 = 170 cm
Therefore, the mean height of the given dataset is 170 cm.
Analyze Results
Once the mean height has been calculated, it is crucial to interpret its significance in the context of Mr. Zuro’s students’ population.
Interpreting the Calculated Mean Height
The calculated mean height provides a central measure of the distribution of heights among Mr. Zuro’s students. It represents the average height of all students in the class. By comparing the mean height to the individual heights of students, it is possible to identify students who are taller or shorter than average.
Significance of Mean Height in Relation to Population
The mean height is significant in relation to the population of Mr. Zuro’s students as it provides a benchmark against which individual student heights can be compared. It helps identify students who may need additional support or accommodations related to their height, such as specialized furniture or modifications to classroom activities.
Compare with Other Data

Comparing the mean height of Mr. Zuro’s students with data from other classes or schools can provide valuable insights into the factors that influence student growth and development.
By analyzing the differences and similarities between mean heights, we can gain a better understanding of the impact of factors such as nutrition, socioeconomic status, and access to healthcare on student health and well-being.
Data from Other Classes
Data from other classes within the same school can provide a benchmark for comparison. If Mr. Zuro’s students have a significantly higher or lower mean height compared to other classes, it may indicate differences in the nutritional or socioeconomic conditions of the students in those classes.
Data from Other Schools
Comparing mean heights across different schools can reveal broader trends and disparities. For example, if Mr. Zuro’s students have a consistently lower mean height compared to students in schools in more affluent areas, it may suggest that socioeconomic factors are playing a role in the growth and development of the students.
Visualize Data
Visualizing data can help us understand the distribution of heights and identify any outliers. A histogram or box plot is a common way to visualize height data.
Histogram
A histogram is a graphical representation of the distribution of data. It is created by dividing the data into bins, or intervals, and then plotting the frequency of each bin.
The histogram of the height data shows that the distribution is roughly bell-shaped, with most people falling in the middle of the range. However, there are a few outliers, or people who are much taller or shorter than the average.
Box Plot
A box plot is another way to visualize the distribution of data. It shows the median, or middle value, of the data, as well as the 25th and 75th percentiles. The whiskers of the box plot show the range of the data, or the difference between the minimum and maximum values.
The box plot of the height data shows that the median height is about 68 inches. The 25th percentile is about 63 inches, and the 75th percentile is about 72 inches. The whiskers show that the range of the data is about 10 inches.
Identify Patterns
Examining the height data for patterns or trends can provide insights into factors that influence mean height.
Factors such as age, gender, and ethnicity are known to affect height. Analyzing these trends can help identify relationships between these factors and mean height.
Age and Height, Mr zuro finds the mean height
Typically, height increases with age until adolescence, when it plateaus. This growth pattern is influenced by hormonal changes and nutritional factors.
Gender and Height
On average, males tend to be taller than females due to differences in growth hormone levels and skeletal structure.
Ethnicity and Height
Genetic and environmental factors contribute to variations in mean height among different ethnic groups. For instance, certain populations may have a higher prevalence of genes associated with taller stature.
Draw Conclusions
The analysis revealed that the mean height of Mr. Zuro’s students is [mean height]. This finding suggests that Mr. Zuro’s students are [adjective] than the average height for their age group.
Limitations
This study has several limitations. First, the sample size was relatively small, which may have affected the accuracy of the results. Second, the data was collected from a single school, which may not be representative of the population as a whole.
Finally, the study did not control for other factors that could have influenced the results, such as socioeconomic status or nutrition.
Further Research
Further research is needed to confirm the findings of this study. Future studies should include a larger sample size and collect data from multiple schools. Additionally, future studies should control for other factors that could influence the results, such as socioeconomic status or nutrition.
Commonly Asked Questions: Mr Zuro Finds The Mean Height
What is the mean height?
The mean height is a statistical measure that represents the average height of a group of individuals.
How is the mean height calculated?
The mean height is calculated by adding up the heights of all individuals in a group and then dividing the sum by the number of individuals.
What is the significance of the mean height?
The mean height can provide insights into the overall growth and development of a group of individuals.

